Ultimative Zahlen: Unterschied zwischen den Versionen
As-sap (Diskussion | Beiträge) |
As-sap (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
{{Inuse|As-sap}} | {{Inuse|As-sap}} | ||
| + | ,die, nicht ,das. | ||
| + | |||
| + | Das Ultimative Zahlen entspricht der Steuernachzahlung (siehe [[Steuern]] und wird hier nicht behandelt. | ||
| + | |||
Die ultimativen Zahlen stellen die Vereinigung aller relevanter Zahlenmengen dar. | Die ultimativen Zahlen stellen die Vereinigung aller relevanter Zahlenmengen dar. | ||
| − | Dazu zählen die reellen Zahlen, die imaginären Zahlen und die paradoxen Zahlen. | + | Dazu zählen die reellen Zahlen, die imaginären Zahlen und die [[paradoxe Zahlen|paradoxen Zahlen]]. |
== Mengenlehre == | == Mengenlehre == | ||
| Zeile 7: | Zeile 11: | ||
<math>U = R \cup I \cup P</math> | <math>U = R \cup I \cup P</math> | ||
| − | Dem aufmerksamen Leser wird nicht entgangen sein, dass sich die reellen Zahlen schon mit den imaginären Zahlen zusammengeschlossen hatten, um die Union der komplexen Zahlen zu bilden. | + | Dem aufmerksamen Leser wird nicht entgangen sein, dass sich die reellen Zahlen schon mit den imaginären Zahlen zusammengeschlossen hatten, um die Union der [[Komplexe Zahlen|komplexen Zahlen]] zu bilden. |
<math>C = R \cup I</math> | <math>C = R \cup I</math> | ||
| Zeile 15: | Zeile 19: | ||
<math>U = C \cup P</math> | <math>U = C \cup P</math> | ||
| − | Jedoch sollte niemals vergessen werden, dass sich in der Menge der komplexen Zahlen insgesamt 3 Untermengen verstecken. Denn jede Komplexe Zahl kann entweder nur reel, nur imaginär oder beides sein. | + | Jedoch sollte niemals vergessen werden, dass sich in der [[Menge]] der komplexen Zahlen insgesamt 3 Untermengen verstecken. Denn jede Komplexe Zahl kann entweder nur reel, nur imaginär oder beides sein. |
| − | Daraus ergibt sich die wahre Union der ultimativen Zahlen, verdeutlich durch | + | Daraus ergibt sich die wahre Union der ultimativen Zahlen, verdeutlich durch Weglassen der Vereinigungszeichen: |
<math>U = C C C P</math> | <math>U = C C C P</math> | ||
| Zeile 25: | Zeile 29: | ||
| − | Während für die komplexen Zahlen ein kartesisches Koordinatensystem ausreichte, erfordern die ultimativen Zahlen eine weitere Dimension. Aufgrund der Eigenheiten der paradoxen Zahlen liegt der Ursprung der paradoxen Ebene nicht im Ursprung der beiden anderen Dimensionen. | + | Während für die komplexen Zahlen ein kartesisches Koordinatensystem ausreichte, erfordern die ultimativen Zahlen eine weitere [[Dimension]]. Aufgrund der Eigenheiten der paradoxen Zahlen liegt der Ursprung der paradoxen Ebene nicht im [[Ursprung]] der beiden anderen Dimensionen. |
Grund: <math>0 \cdot p = p^{-1} \cdot p = 1</math> | Grund: <math>0 \cdot p = p^{-1} \cdot p = 1</math> | ||
| Zeile 31: | Zeile 35: | ||
== Anwendungsbeispiel == | == Anwendungsbeispiel == | ||
| − | Mit ultimativen Zahlen kann man auch ultimativ rechnen. Als gemeines Beispiel sei hier folgende Funktion herangezogen: | + | Mit ultimativen Zahlen kann man auch ultimativ rechnen. Als gemeines Beispiel sei hier folgende [[Funktion]] herangezogen: |
<math>f(x) = \frac{Sin(x)}{x}</math> | <math>f(x) = \frac{Sin(x)}{x}</math> | ||
| Zeile 44: | Zeile 48: | ||
Das Ergebnis ist also 1! | Das Ergebnis ist also 1! | ||
| + | {{Zahlen}} | ||
[[Kategorie:Zahlen]] | [[Kategorie:Zahlen]] | ||
[[Kategorie:Mathematik]] | [[Kategorie:Mathematik]] | ||
Version vom 4. Dezember 2007, 19:07 Uhr
 |
Dieser Artikel ist in Arbeit • Letzte Bearbeitung: 04.12.2007
Hier nimmt As-sap Änderungen vor. Falls Du etwas dazu beitragen willst, melde Dich bitte in der Autorendiskussion oder in der Seitendiskussion. Nimm keine eigenmächtigen Änderungen vor, bis dieser Baustein vom Autor entfernt wurde. |
 |
,die, nicht ,das.
Das Ultimative Zahlen entspricht der Steuernachzahlung (siehe Steuern und wird hier nicht behandelt.
Die ultimativen Zahlen stellen die Vereinigung aller relevanter Zahlenmengen dar. Dazu zählen die reellen Zahlen, die imaginären Zahlen und die paradoxen Zahlen.
Mengenlehre
[math]U = R \cup I \cup P[/math]
Dem aufmerksamen Leser wird nicht entgangen sein, dass sich die reellen Zahlen schon mit den imaginären Zahlen zusammengeschlossen hatten, um die Union der komplexen Zahlen zu bilden.
[math]C = R \cup I[/math]
Daraus ergibt sich
[math]U = C \cup P[/math]
Jedoch sollte niemals vergessen werden, dass sich in der Menge der komplexen Zahlen insgesamt 3 Untermengen verstecken. Denn jede Komplexe Zahl kann entweder nur reel, nur imaginär oder beides sein.
Daraus ergibt sich die wahre Union der ultimativen Zahlen, verdeutlich durch Weglassen der Vereinigungszeichen:
[math]U = C C C P[/math]
Koordinatensystem
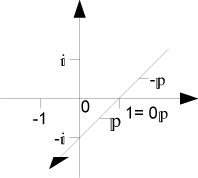
Während für die komplexen Zahlen ein kartesisches Koordinatensystem ausreichte, erfordern die ultimativen Zahlen eine weitere Dimension. Aufgrund der Eigenheiten der paradoxen Zahlen liegt der Ursprung der paradoxen Ebene nicht im Ursprung der beiden anderen Dimensionen.
Grund: [math]0 \cdot p = p^{-1} \cdot p = 1[/math]
Anwendungsbeispiel
Mit ultimativen Zahlen kann man auch ultimativ rechnen. Als gemeines Beispiel sei hier folgende Funktion herangezogen: [math]f(x) = \frac{Sin(x)}{x}[/math]
Im reellen Zahlenraum musste man sich noch eines Tricks (dem Limes) behelfen, um den Funktionswert bei x = 0 zu bestimmen. Im ultimativen Zahlenraum geht das viel einfacher:
[math]\frac{Sin(x)}{x}, x = 0 \Rightarrow p \cdot Sin(p^{-1})[/math]
Da [math]Sin(p^{-1}) = Sin(0)[/math] ist und der Sinus an der Stelle 0 0 ergibt:
[math]p \cdot 0 = p \cdot p^{-1} = 1[/math]
Das Ergebnis ist also 1!
Einstellige Zahlen:
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9
Ausgewählte zweistellige Zahlen:
10 |
11 |
12 |
13 |
14 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
30 |
32 |
42 |
50 |
69 |
88 |
90 |
96 |
99
Weitere wichtige Zahlen
0190 | 0900156661317 | 1/2 | 50 % | 99,9 % | 100 % | 103,9 % | 1,95583 | 3 1/2 | 4,67288327381920102 | 5:45 | 6,4 | 7,87678 | 08/15 | 10,5 | 54-74-90-2006 | 87,5 | 90-60-90 | 300 | 333 | 666 | 667 | 700 | 911 | 1313 | 1337 | 1757 | 2379 | 40200 | 89547 | 126025 | 1.000.000 | 1.000.000.000 | 1234567890 | 93278329324 | 1.000.000.000.000 | 702 Dezilliarden 432 Octilliarden 666 Septillionen 74 Quintilliarden 907 Quadrilliarden 4 Milliarden 728 Tausend 332,344 Periode
Anderthalb | API | Arbeitslosenzahl | Drölf | Drölfzehn | Dunkelziffer | Einzahl | Eulersche Zahl | Fuffzich | Fümpf | Hundert | Keine Lösung | NaN | Normalnull | Nullzig | Nullundnullzig | Nummer | Pi | Postleitzahl | Tausend | Unendlich | Urnull | Urzahl | Vacht | Vielzahl | Zahl | Zufallszahl | Zweins | Zwünf